Pagina 1 di 1
[Cesenatico 2016 - 3] Intersezioni eccentriche
Inviato: 09 mag 2016, 22:32
da Talete
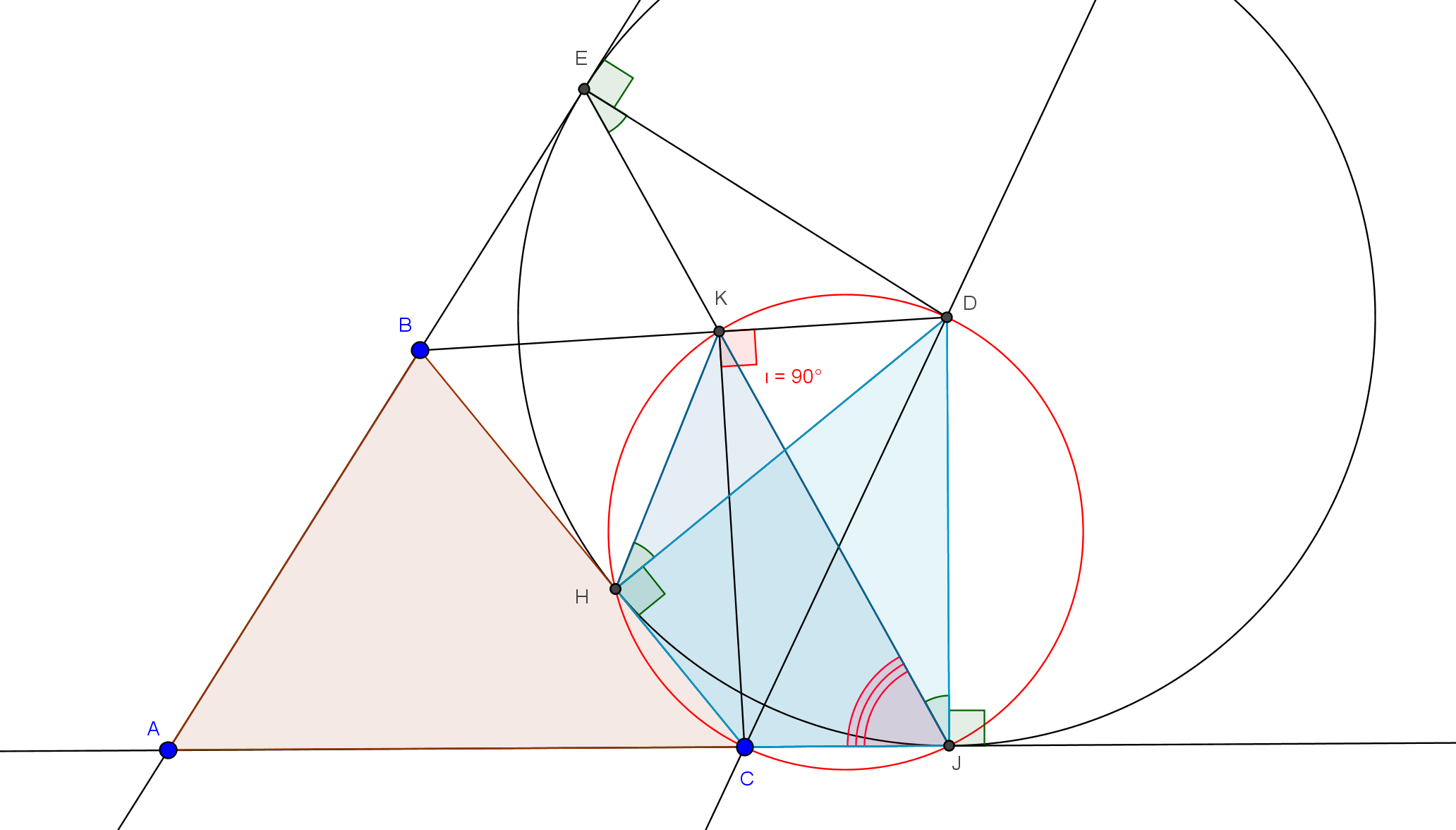
Sia $\Gamma$ la circonferenza ex-inscritta al triangolo $ABC$ opposta al vertice $A$, ossia la circonferenza tangente a $BC$ e ai prolungamenti dei lati $AB$ e $AC$ dalla parte di $B$ e di $C$. Sia $D$ il centro di $\Gamma$ e siano $E$ ed $F$, rispettivamente, i punti di tangenza di $\Gamma$ con i prolungamenti dei lati $AB$ ed $AC$. Sia $J$ l'intersezione tra i segmenti $BD$ ed $EF$.
Dimostrare che l'angolo $\angle CJB$ è retto.
Re: [Cesenatico 2016 - 3] Intersezioni eccentriche
Inviato: 10 mag 2016, 13:25
da EELST
Si fa benissimo invertendo, vero zetaeffe ??

Re: [Cesenatico 2016 - 3] Intersezioni eccentriche
Inviato: 10 mag 2016, 15:13
da zetaeffe
Ahahahah

Re: [Cesenatico 2016 - 3] Intersezioni eccentriche
Inviato: 13 mag 2016, 00:21
da Lasker
La mia soluzione è talmente triste che sento di doverla postare
Re: [Cesenatico 2016 - 3] Intersezioni eccentriche
Inviato: 09 giu 2016, 20:34
da zarok
ho provato a invertire rispetto l'ex-inscritta ma non mi viene...devo provare un'altra inversione o è questa la strada giusta? Si accettano suggerimenti
Re: [Cesenatico 2016 - 3] Intersezioni eccentriche
Inviato: 09 giu 2016, 22:25
da zetaeffe
Premettendo che l'inversione non è la strada più veloce

, ecco qualche hint:
Hint 1:
Hint 2:
Hint 3:
Hint 4:
Re: [Cesenatico 2016 - 3] Intersezioni eccentriche
Inviato: 10 giu 2016, 00:14
da Talete
E dire che avevo pure provato ad invertire in gara, e avevo beccato anche la circonferenza giusta! Poi, il fascino delle baricentriche... mi ha portato alla bellezza di 1 misero punto. Amen.
Ora provo a risolverlo con l'inversione!
EDIT: Maledizione, con gli hint di ZF ce l'ho fatta... complimenti, bella soluzione!
Re: [Cesenatico 2016 - 3] Intersezioni eccentriche
Inviato: 10 giu 2016, 00:59
da gpzes
- cese2016.png (135.69 KiB) Visto 4520 volte