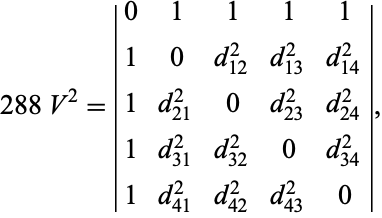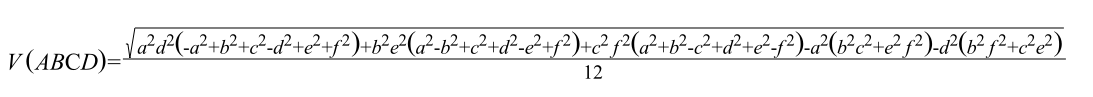Sono nuovo (ma vecchio di età e di frequenza in forum di carattere matematico).
Mi sono inscritto perché, dopo aver trovato per conto mio una formula per il volume del tetraedro irregolare, ho cercato se c'era a proposito qualcosa in rete ed ho trovato questo
"thread" ... che mi pare interessante ma anche di poca utilità pratica (se non si ha una applicazione che sappia fare sbrigativamente determinanti di matrici quadrate di formato 5 x 5 (che, se fatti secondo la definizione, conducono a ben 120 addendi).
EvaristeG ha scritto: ↑31 lug 2006, 22:28
Sì, c'è : Cayley-Menger!
$ 288V^2=\left|\begin{array}{ccccc}0&1&1&1&1\\
1&0&a^2&b^2&c^2\\1&a^2&0&d^2&e^2\\1&b^2&d^2&0&f^2\\
1&c^2&e^2&f^2&0\end{array}\right| $
con a, b, c, d, e, f spigoli del tetraedro.
Queste informazioni non bastano!
Questo determinante non è invariante ad ogni permutazione della sestupla [a, b, c, d, e, f].
Voglio dire: bisogna anche sapere come è messo uno spigolo rispetto agli altri!
Precisamente:
• dato uno spigolo qualunque, siccome ognuno dei 4 vertici è estremo di tre spigoli, ci sono altri 4 spigoli con un estremo comune al dato spigolo ed un solo spigolo senza estremo comune. Diciamo che il dato spigolo e quello senza estremo comune sono
"opposti" (uno dsell'altro).
• Delle 15 coppie dei suoi 6 spigoli, 3 coppie sono di "
spigoli opposti" , ossia non complanari" e 11 sono coppie di spigoli complanari.
Delle 20 terne di spigoli
• 4 terne sono di spigoli con un estremo comune [in uno dei 4 vertici]:
• 4 terne sono di spigoli complanari [lati di una delle 4 facce];
• le altre 12 terne sono ripartibili in 3 quaterne di terne comprendono una coppia di spigoli opposti ed uno spigolo con un vertice comune al primo ed un vertice comune al secondo dei due spigoli opposti. Quindi in ciascuna di queste quaterne di terne figurano tutti i 6 spigoli; ed in ciasscuna di queste terne ci sono tutti i 4 vertici (che a tre a tre individuano le 4 facce).
Un modo di evitare gli equivoci è quello di indicare con 1, 2, 3 e 4 i vertici e e con
d
12, d
13, d
14, d
23, d
24, d
34
le lunghezze dei 6 spigoli (di estremi due dei 4 vertici).
Il determinante di Cayley-Menger! per lospazio tridimensionale dà infatti:
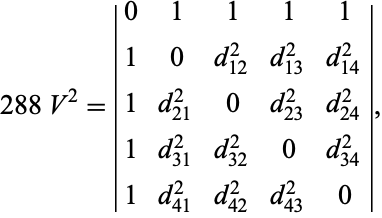
Ma anche questo non è di rapido impiego!
------------
Siano note le lunghezze dei singoli spigoli di un tetraedro.
Ho trovato che, in generale, il volume è un dodicesimo della radice quadrata di una somma di 22 monomi dei quali 12 sono positivi (a coefficiente 1) e 10 sono negativi (a coefficiente –1).
[Più sotto spiegherò come si arriva facilmente a questo risultato].
Adesso spiego, appoggiandomi ad un modello, come determinare ciascuno dei 22 addendi sella somma sotto radice quadrata
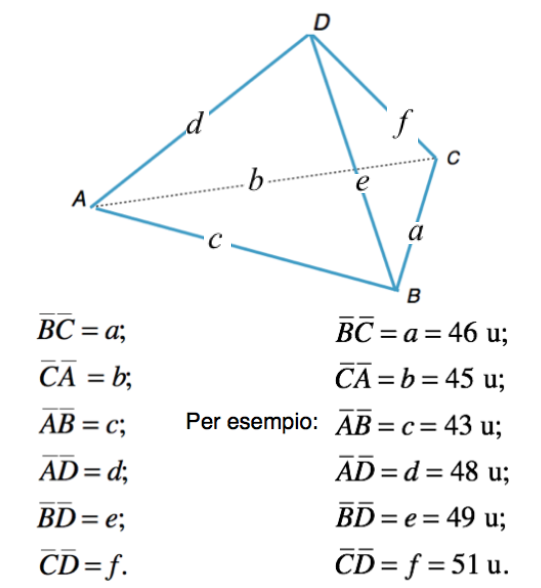
Pensiamo (per comodità) il tetraedro
ABCD come una piramide triangolare di base
ABC e vertice
D.
Le lunghezze degli spigoli siano le seguenti:
BC =
a;
CA =
b;
AB =
c;
AD =
d;
BD =
e;
CD =
f.
Evidentemente le coppie di vertici opposti sono allora: [a, d]; [b, e]; [c, f].
Le terne di spigoli lati di una delle 4 facce sono [a, b, c]; [a, e, f]; [b, d, f]; [c, d, e].
Tenute presenti le posizioni degli spigoli, ecco l'algoritmo per scrivere i 22 addendi della somma sotto radice quadrata
a) Ogni volta che compare una delle 6 lettere [indeterminate] essa figura al quadrato.
b) Per ciascuna delle tre coppie di opposti scriviamo il prodotto dei dei quadrati dei due spigoli opposti e moltoplichiamo per la somma dei quadrati di tutti i 6 spigoli cambiando però poi il segno da "+" a "–" dei quadratri degli sterssi spigoli opposti.
Per esempio, per la coppia di spigoli opposti [a, d] abbiamo:
(a^2)·(d^2)·[–a^2 + b^2 + c^2 – d^2 + e^2 + f^2].
Per la coppia di spigoli opposti [b, e] abbiamo:
(b^2)·(e^2)·[a^2 – b^2 + c^2 + d^2 - e^2 + f^2].
E per la coppia di spigoli opposti [c, f] abbiamo:
(c^2)·(f^2)·[a^2 + b^2 - c^2 + d^2 + e^2 - f^2].
Naturalmente di queste tre espressioni facciamo la somma.
c)[/c] Alla somma di questi 18 termini sottraiamo i 4 prodotti dei quadrati dei 3 lati delle 4 facce; ossia aggiungiamo:
– [(abc)^2 + (aef)^2 +(bdf)^2 + (cde)^2]
c)[/c] Facciamo la radice quadrata dell'intera somma e dividiamo per 12.
Ho fatto un'immagine del detto modello di tetraedro ed un'altra dell'espressione del volume:
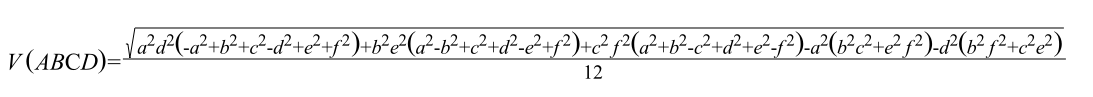
–––––––––––––
Spiego ora come si arriva a quella formula.
1) Si ricordi che in un triangolo di vertici A, B e C e lati rispettivamente opposti a, b e c, i coseni degli angoli x, y e z di vertici rispettivi A, B e C sono:
cos(x) = (b^2 + c^2 – a^2)/(2bc); cos(y) = (c^2 + a^2 – b^2)/(2ca); cos(z) = (a^2 + b^2 – c^2)/(2ab). [*][/b]
2) Un triedro abbia le facce di angoli φ, χ e ψ e gli angoli diedri rispettivamente oppoasti siano α, β e γ. Allora il
"1° teorema del coseno" della "Trigonometria sferica" permette di calcolare un angolo diedro in funzione degli angoli delle facce.In formule si ha:
cos(α) = [cos(φ) –cos(χ)·cos(ψ)]/[sin(χ)·sin(ψ)];
cos(β) = [cos(χ) –cos(ψ)·cos(φ)]/[sin(ψ)·sin(φ)];
[**]
cos(γ) = [os(ψ) - cos(φ·cos(χ))]/[sin(φ)·sin(χ)].
Nella figura del tetraedro di sopra siano:
φ l'amgolo in
A di lati
b e
c;
χ l'aamgolo in
A di lati
b e
d;
ψ langolo in
Adi lati
c e
d:
β l'angolo diedro di spigolo
AB =
c.
Allora il coseno dell'angolo
β vale (come dice la
[**]): cos(β) = [cos(χ) –cos(ψ)·cos(φ)]/[sin(ψ)·sin(φ)]. E di conseguensa si ha:
sin(β) =√{1 – [cos(β)]^2} = √{1 – [cos(φ)]^2 – [cos(χ)]^2 – [cos(ψ)]^2 + 2cos(φ)·[cos(χ)·cos(ψ)}/[[sin(ψ)·sin(φ)].
[***]
Pertanto la distanza
h di
D dal piano della faccia
ABC vale:
h = d·[sin(ψ)·sin(β)] = d·√{1 – [cos(φ)]^2 – [cos(χ)]^2 – [cos(ψ)]^2 + 2cos(φ)·cos(χ)·cos(ψ)}/[sin(φ)].
E siccome l'area della faccia
ABC vale [b·c·sin(φ)]/2, il volume del tetraedro ABCD della figura di sopra vale:
V = <area di
ABC>·h/3 = bcd·{1 – [cos(φ)]^2 – [cos(χ)]^2 – [cos(ψ)]^2 + 2cos(φ)·[cos(χ)·cos(ψ)}/6.
E' dunque facile (ancorché noioso!) sostituire in questa formula le funzioni circolari cos(φ), cos(χ) e cos(ψ) con le loro espressioni razionali nelle variabili "lunghezze degli spigoli" (secondo lo schema
[**]) In tal modo si ottiene la formula mostrata nella seconda immagine (e precedentemente spiegata in riferimento alla mutua posizione dei singoli spigoli).
_________