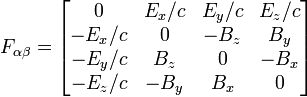OliForum Matematico

Un elettrone con carica $ \displaystyle q $, velocità $ \displaystyle v $ confrontabile con $ \displaystyle c $ e massa $ \displaystyle m $ si muove in un campo magnetico $ \displaystyle B $ uniforme e costante, perpendicolarmente alle linee del campo.
Dimostrare che il percorso circolare su qui si muove l'elettrone nel campo ha raggio:

$ \displaystyle r = \frac{mv}{qB \sqrt{1-(\frac{v}{c})^2}} $

Innanzitutto, una particella di carica $ ~q $, con velocità $ ~ \stackrel {\rightarrow}{v} $, che si muove in un campo magnetico $ ~ \stackrel {\rightarrow}{B} $ è soggetta alla forza di Lorentz:

$ ~ \stackrel {\rightarrow}{F} = q \stackrel {\rightarrow}{v} \wedge \stackrel {\rightarrow}{B} $

Il modulo è quindi:

$ ~ F = qvB\sin{\alpha} $

Dove $ ~\alpha $ è l'angolo che la direzione del moto forma con il vettore $ ~ \stackrel {\rightarrow}{B} $. Se la direzione del moto è ortogonale al campo, ci riduciamo a:

$ ~ F = qvB $

Come da problema, i vettori $ ~\stackrel {\rightarrow}{v} $ e $ ~ \stackrel {\rightarrow}{B} $ sono ortogonali. Dato che il vettore $ ~\stackrel {\rightarrow}{F} $ è sempre ortogonale a tutti e due, i tre vettori formano una terna ortogonale destrorsa. Il vettore spostamento ha lo stesso verso e direzione del vettore $ ~ \stackrel {\rightarrow}{v} $, quindi è anch'esso ortogonale alla forza di Lorentz, il che implica che il lavoro compiuto è nullo, ed è nulla anche la variazione di energia cinetica, quindi la velocità è costante in modulo. Dato che $ ~\stackrel {\rightarrow}{v} $ e $ ~\stackrel {\rightarrow}{F} $ sono perpendicolari, allora varierà la direzione, creando quindi un moto circolare uniforme. Se noi vedessimo il campo magnetico uscire dal piano di visione verso di noi, una particella a carica positiva girerebbe in senso orario (si trova ciò con la regola della mano sinistra). Dato che nel problema la particella è un elettrone, la carica è negativa e la forza ha verso opposto. Quindi cambia il senso, che ora è antiorario. La particella si muoverà di moto circolare uniforme lungo una circonferenza di raggio $ ~r $. La particella subirà anche una accelerazione centripeta $ ~a_c $ diretta verso il centro di rotazione, con lo stesso verso e direzione di $ ~\stackrel {\rightarrow}{F} $, e di modulo:

$ \displaystyle a_c=\frac {v^2}{r} $

Per la 2° Legge della Dinamica avremo una forza centripeta di modulo:

$ \displaystyle F=\frac {mv^2}{r} $

È evidente che la forza centripeta è la forza di Lorentz, quindi si possono eguagliare le due espressioni:

$ \displaystyle qvB=\frac {mv^2}{r} $

E ricavando $ ~r $:

$ \displaystyle r=\frac {mv}{qB} $

Tutto il discorso fatto vale se $ ~v \ll c $. Se $ ~v $ comincia a diventare confrontabile con $ ~c $ allora bisogna effettuare una correzione alla formula di $ ~r $. Questo ce lo permette la relazione di Einstein:

$ \displaystyle m(v) = \frac{m_0}{\sqrt{1-(\frac{v}{c})^2}} $

Dove $ ~m_0 $ è la massa della particella a riposo. Si vede che $ ~m $ è in funzione di $ ~v $, varia al variare di quest'ultima. Finchè $ ~v\ll c $ il denominatore è molto prossimo a 1, da ciò $ ~ m \simeq m_0 $. Quando $ ~v $ comincia a diventare prossima a $ ~c $, abbiamo che l'approssimazione precedente non è più applicabile, $ ~m \neq m_0 $. Da ciò, visto che la $ ~m $ nell'espressione del raggio è quella che ha la particella a velocità $ ~v $, dobbiamo effettuare la sostituzione con la relazione di Einstein. Così si arriva alla formula iniziale per il raggio:

$ \displaystyle r = \frac{m_0v}{qB \sqrt{1-(\frac{v}{c})^2}} $

Ciao!

Jonny Tendenza ha scritto:Questo ce lo permette la relazione di Einstein:

$ \displaystyle m(v) = \frac{m_0}{\sqrt{1-(\frac{v}{c})^2}} $

Dove $ ~m_0 $ è la massa della particella a riposo.

Mi spieghi un attimo come funziona questa legge? Nel capitolo dell'Halliday sulla relatività non l'ho trovata...

Quindi con la relatività la seconda legge di Newton diventa

$ \displaystyle \vec{F} = m(v) \vec{a} = \frac{m_0}{\sqrt{1-\beta ^2}} \vec{a} $

...Giusto?

Sull'Halliday stranamente non viene spiegata esplicitamente (e nè tantomeno citata) la variazione di massa inerziale a velocità confrontabili con $ ~c $; viene dimostrata solo la formula relativistica della quantità di moto, che si ottiene aggiungendo il fattore di Lorentz alla formula classica ($ p=\gamma m v $). La forma relativistica della seconda legge di Newton può essere ricavata allo stesso modo.

Si parte dalla forma classica $ \displaystyle F=ma=m \frac {dv}{dt_0} $ in cui $ dt_0 $ è l'intervallo di tempo misurato da un osservatore solidale col corpo in moto, ed è uguale, secondo la legge di dilatazione dei tempi, a $ \displaystyle \frac {dt}{\gamma} $. Sostituendo si giunge quindi a $ \displaystyle F=m \gamma \frac {dv}{dt}= \gamma m a $, che è esattamente la formula che hai scritto tu.

La dinamica relativistica è un po' più complicata della semplice sostituzione $ m \rightarrow \gamma m $. Il fatto che il tempo sia "promosso" da parametro a coordinata rende le equazioni del moto "quadridimensionali", mentre quelle di Newton sono tridimensionali. Inoltre si può dimostrare (è un risultato piuttosto complicato, e senza tecniche avanzate non posso dare nemmeno l'idea di come ci si arriva) che la relatività ristretta è incompatibile con una dinamica che preveda "azioni a distanza": l'unica interazione che può esserci è "di contatto" (è quello che rende necessario introdurre il concetto di campo), quindi viene meno la necessità di mantenere il concetto stesso di forza, e questo è il motivo per cui nella maggior parte dei libri non vi si accenna nemmeno.

Provo a dare un'idea di cosa sia la dinamica relativistica e di come si trattano i campi elettromagnetici. Per maggiori dettagli potete guardare un paio di libri che fanno una trattazione non eccessivamente avanzata (ma che comunque richiede qualche nozione di algebra lineare e di analisi):
Goldstein, Classical Mechanics
Landau, Teoria dei Campi

D'ora in poi pongo $ c = 1 $, per comodità e perchè altrimenti prima o poi me ne dimentico.
Supponiamo che $ (x^0 = t, x^1,x^2,x^3) $ siano le coordinate di un determinato sistema di riferimento, che chiameremo "del laboratorio". Il tempo proprio di un corpo, cioè il tempo misurato in un sistema solidale col moto del corpo, è "definito" da $ dt = \gamma d\tau $. D'ora in poi il tempo proprio lo indicherò con $ s $. Possiamo allora definire alcuni quadrivettori: la traiettoria di una particella, "parametrizzata rispetto al tempo proprio", sarà descritta da 4 funzioni: $ x^i = x^i(s) $. Allora possiamo definire la quadrivelocità:
$ \displaystyle U^i = { dx^i \over ds} $
E il quadrimpulso : $ P^i = mU^i $
dove $ m $ è la massa a riposo... Quello che si può verificare facilmente è che, se $ \vec{v} $ è la velocità nel sistema di riferimento del laboratorio, allora
$ U^i = (\gamma, \gamma \vec{v}) $ e $ P^i = (E, \vec{p}) $, dove $ \gamma = {1 \over \sqrt{1 - v^2}} $.

Veniamo ora all'elettromagnetismo. Dobbiamo riscrivere anche questo in forma quadrimensionale: in realtà è la forma più naturale in cui scriverlo (tant'è che la relatività è stata sviluppata prima di tutto per risolvere le contraddizioni di meccanica classica ed elettromagnetismo). Per fare questo introduciamo il tensore elettromagnetico $ F_{ij} $ che si può scrivere nella forma



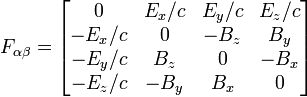
Prima di scrivere le equazioni del moto una questione di notazione: se ho due quadrivettori $ A^i, B^i $ il loro "prodotto scalare" è
$ \displaystyle A^iB_i = A_iB^i = \sum_{i=0}^3 g_{ij}A^iB^i $
con $ g_{ij} = g^{ij} $ (attenzione! l'uguaglianza vale solo in relatività ristretta, in realtà le due matrici - quella con gli indici in alto e quella con gli indici in basso - sono l'una l'inversa dell'altra) la matrice diagonale che ha come elementi della diagonale $ (1, -1, -1, -1) $. Sottolineo il fatto che nella notazione che adotterò è sottointesa la somma sugli indici ripetuti. Gli indici si alzano e abbassano in questo modo:
$ A^i = g^{ij}A_j $, $ B_i = g_{ij}B^j $

Detto questo, le equazioni del moto sono:
$ \displaystyle {dU^i \over ds} + eF^{ij}U_j = 0 $
dove $ e $ è la carica della particella. Se si fa uno sviluppo al primo ordine nella velocità si può dimostrare che questa equazione si riduce alla legge di Lorentz.

Ok... tutto questo (di cui non so quanto si sarà capito) per dire che non basta sostituire la massa nella legge di Newton: si vede (abbastanza bene credo) dalle equazioni del moto. Infatti la velocità dipende dal tempo proprio, di conseguenza l'equazione differenziale è non lineare in $ v $, infatti c'è un $ \gamma $ nella definizione della quadrivelocità. Quindi il modo in cui la relatività modifica le equazioni del moto è non banale; si vede anche bene come la componente temporale non possa essere "disaccoppiata" dal quelle spaziali.
Beh, ora avete le equazioni corrette... potete risolvere l'esercizio anche nel caso relativistico