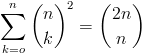Messaggio
da Jessica92 »
Io conosco questa:
$ $(a-b)^{2n}= \sum_{i=0}^n {2n \choose i}a^i(-b)^{2n-i} $
Quindi il coefficente di $ a^n(-b)^n $sarà $ $2n \choose n $
Ma $ $(a-b)^{2n}=(a-b)^n(a+b)^n= \sum_{i=0}^n {n \choose i}a^i(-b)^{n-i} \sum_{j=0}^n {2n \choose j}a^jb^{n-j} $
E il coefficiente di $ a^n(-b)^n $ sarà $ $\sum_{i,j\geq0\ i+j=n}^n {n \choose i}{n \choose j}=\sum_{i=0}^n {n \choose i}^2 $
Poichè $ ${n \choose i} = {n \choose n-i} $
E quindi
$ $ \sum_{i=0}^n {n \choose i}^2 = {2n \choose n} $